Осёл-картёжник — различия между версиями
Mook monk (обсуждение | вклад) (→Отсылки) |
Mook monk (обсуждение | вклад) (→Минутка научпопа) |
||
| Строка 28: | Строка 28: | ||
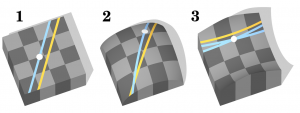
Все мы в школе изучаем геометрию Евклида, пятый и последний постулат которой можно сформулировать следующим образом: «Через точку, лежащую вне прямой, можно провести одну и только одну прямую, не пересекающуюся с ней». | Все мы в школе изучаем геометрию Евклида, пятый и последний постулат которой можно сформулировать следующим образом: «Через точку, лежащую вне прямой, можно провести одну и только одну прямую, не пересекающуюся с ней». | ||
| − | В XIX веке пытливые умы попробовали построить альтернативную, неевклидову геометрию, изменив пятый постулат. В геометрии Римана через упомянутую выше точку нельзя было провести ни одной прямой (все параллельные прямые пересекались), а в геометрии Лобачевского — сколько угодно (прямые не пересекались). Эта игра ума оказалась не только внутренне непротиворечивой, но и хорошо подошла к физической | + | В XIX веке пытливые умы попробовали построить альтернативную, неевклидову геометрию, изменив пятый постулат. В геометрии Римана через упомянутую выше точку нельзя было провести ни одной прямой (все параллельные прямые пересекались), а в геометрии Лобачевского — сколько угодно (прямые не пересекались). Эта игра ума оказалась не только внутренне непротиворечивой, но и хорошо подошла к описанию физической картины мира, в котором мы живём. |
И да, у Лобачевского параллельные прямые не пересекаются. Они пересекаются у Римана. | И да, у Лобачевского параллельные прямые не пересекаются. Они пересекаются у Римана. | ||
Версия 19:40, 9 сентября 2019
Осёл-картёжник — персонаж романа «Золотой ключ».
Впервые упоминается в Интроспекции учёной, где он пытается развести Карло Коллоди на партеечку-другую:
Есть, правда, один осёл. Интересный тип. Хоть из электората, но жизнь видел, байки травит хорошо. Однако картёжник заядлый. И к тому же шулер. Так что садиться с ним играть никому не советую. Он меня спервоначала тоже подбивал — давай, дескать, в подкидного, на просто так. Ага, будто я не знаю, что в вольерах «просто так» — это значит жопа. Ну, я ему объяснил, что на жопу не играю. Я всё-таки доктор Карло Коллоди, а не пседропейник какой-нибудь перепончатый. Он заднего дал: да я чё, да я ничё, да я в хорошем смысле. Но всё ещё надежды не утратил меня подловить, натрибуквыш этакий.
В Действии шестьдесят седьмом Коллоди и кролик Роджер, озверев от скуки, всё же играют с ослом в покер:
Первым вскрылся доктор. У него был фулл-хаус на восьмёрках и двух тузах. Он уже ухмылялся в усы, когда кролик со словами «а вот позвольте-ка вам объебосиков в напёздок присуёбить» выложил трёх королей и две шестёрки. Осёл гаденько ухмылялся. У него, видимо, был стрит-флеш.
Краткая характеристика
Осёл был с виду хуй простой, а на деле — Лобачевский и Риман в одном флаконе. Во всяком случае, в картах. Тут у него и параллельные внезапно пересекались, и теория вероятности нервно курила в закутке. Все, конечно, думали, что осёл жульничает. Но поймать его на этом никому ещё не удавалось. Некоторые подозревали, что ослик — телепат. Однако телепат, даже слабенький, уж точно не поехал бы в археологическую экспедицию простым кашеваром — а осёл вот поехал. К тому же никакой особенной телепачьей проницательности он не проявлял. Разве что умел хорошо подкатывать и убалтывать на «одну партейку». К тому же он садился за любую игру, от сики до перфоманса. Поэтому многие продолжали — с упорством, достойным лучшего применения — с ним играть. То есть проигрывать.
Источник везения
Под нажимом Роджера осёл рассказывает свою историю. Раньше его пялил — и в карты, и в прямом смысле — какой-то вербляд. Но случайно ему встретилась маленькая-миленькая белая кошечка с крылышками, которая посулила, что у него всё наладится, причём по обеим линиям: и картёжной, и интимной.
В карты с тех пор ослу начало везти. А вот в любви не склалось.
Минутка научпопа
Все мы в школе изучаем геометрию Евклида, пятый и последний постулат которой можно сформулировать следующим образом: «Через точку, лежащую вне прямой, можно провести одну и только одну прямую, не пересекающуюся с ней».
В XIX веке пытливые умы попробовали построить альтернативную, неевклидову геометрию, изменив пятый постулат. В геометрии Римана через упомянутую выше точку нельзя было провести ни одной прямой (все параллельные прямые пересекались), а в геометрии Лобачевского — сколько угодно (прямые не пересекались). Эта игра ума оказалась не только внутренне непротиворечивой, но и хорошо подошла к описанию физической картины мира, в котором мы живём.
И да, у Лобачевского параллельные прямые не пересекаются. Они пересекаются у Римана.
Отсылки
- Существует ироничная фраза «Не везёт в картах, повезёт в любви», которую обычно применяют, чтобы насыпать соль на рану проигравшему — или, напротив, приободрить его. В случае с ослом имеет место инверсия: тому везёт в картах, но не везёт в любви.